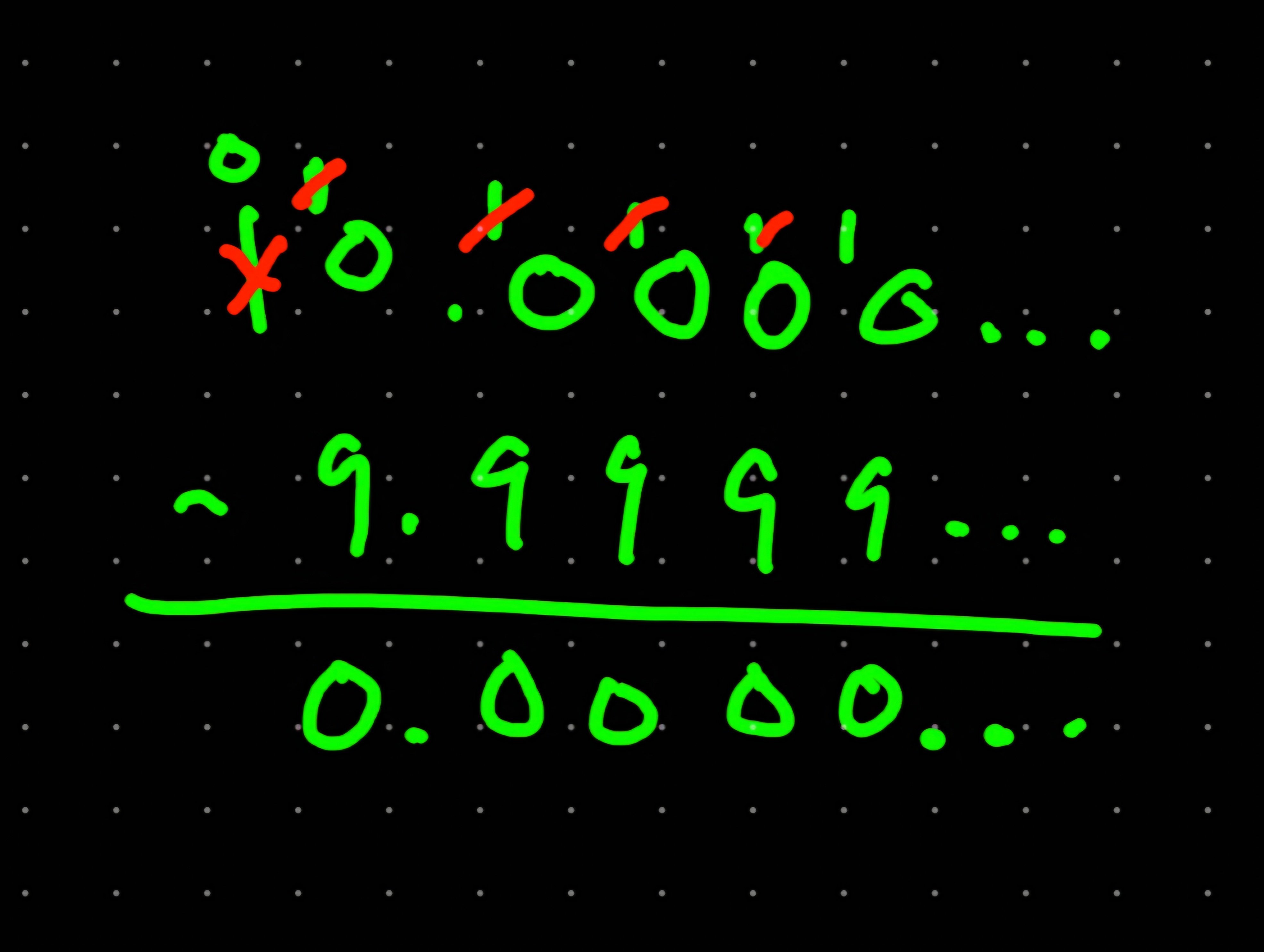
x=.9999…
10x=9.9999…
Subtract x from both sides
9x=9
x=1
There it is, folks.
Somehow I have the feeling that this is not going to convince people who think that 0.9999… /= 1, but only make them madder.
Personally I like to point to the difference, or rather non-difference, between 0.333… and ⅓, then ask them what multiplying each by 3 is.
Oh shit, don’t think I saw that before. That makes it intuitive as hell.
The thing is 0.333… And 1/3 represent the same thing. Base 10 struggles to represent the thirds in decimal form. You get other decimal issues like this in other base formats too
(I think, if I remember correctly. Lol)
Cut a banana into thirds and you lose material from cutting it hence .9999
That’s not how fractions and math work though.
I’d just say that not all fractions can be broken down into a proper decimal for a whole number, just like pie never actually ends. We just stop and say it’s close enough to not be important. Need to know about a circle on your whiteboard? 3.14 is accurate enough. Need the entire observable universe measured to within a single atoms worth of accuracy? It only takes 39 digits after the 3.
pi isn’t even a fraction. like, it’s actually an important thing that it isn’t
pi=c/d
it’s a fraction, just not with integers, so it’s not rational, so it’s not a fraction.
The problem is, that’s exactly what the … is for. It is a little weird to our heads, granted, but it does allow the conversion. 0.33 is not the same thing as 0.333… The first is close to one third. The second one is one third. It’s how we express things as a decimal that don’t cleanly map to base ten. It may look funky, but it works.
Pi isn’t a fraction (in the sense of a rational fraction, an algebraic fraction where the numerator and denominator are both polynomials, like a ratio of 2 integers) – it’s an irrational number, i.e. a number with no fractional form; as opposed to rational numbers, which are defined as being able to be expressed as a fraction. Furthermore, π is a transcendental number, meaning it’s never a solution to
f(x) = 0, wheref(x)is a non-zero finite-degree polynomial expression with rational coefficients. That’s like, literally part of the definition. They cannot be compared to rational numbers like fractions.Every rational number (and therefore every fraction) can be expressed using either repeating decimals or terminating decimals. Contrastly, irrational numbers only have decimal expansions which are both non-repeating and non-terminating.
Since
|r|<1 → ∑[n=1, ∞] arⁿ = ar/(1-r), and0.999...is equivalent to that sum witha = 9andr = 1/10(visually,0.999... = 9(0.1) + 9(0.01) + 9(0.001) + ...), it’s easy to see after plugging in,0.999... = ∑[n=1, ∞] 9(1/10)ⁿ = 9(1/10) / (1 - 1/10) = 0.9/0.9 = 1). This was a proof present in Euler’s Elements of Algebra.There are a lot of concepts in mathematics which do not have good real world analogues.
i, the _imaginary number_for figuring out roots, as one example.
I am fairly certain you cannot actually do the mathematics to predict or approximate the size of an atom or subatomic particle without using complex algebra involving i.
It’s been a while since I watched the entire series Leonard Susskind has up on youtube explaining the basics of the actual math for quantum mechanics, but yeah I am fairly sure it involves complex numbers.
i has nice real world analogues in the form of rotations by pi/2 about the origin (though this depends a little bit on what you mean by “real world analogue”).
Since i=exp(ipi/2), if you take any complex number z and write it in polar form z=rexp(it), then multiplication by i yields a rotation of z by pi/2 about the origin because zi=rexp(it)exp(ipi/2)=rexp(i(t+pi/2)) by using rules of exponents for complex numbers.
More generally since any pair of complex numbers z, w can be written in polar form z=rexp(it), w=uexp(iv) we have wz=(ru)exp(i(t+v)). This shows multiplication of a complex number z by any other complex number w can be thought of in terms of rotating z by the angle that w makes with the x axis (i.e. the angle v) and then scaling the resulting number by the magnitude of w (i.e. the number u)
Alternatively you can get similar conclusions by Demoivre’s theorem if you do not like complex exponentials.
pie never actually ends
I want to go to there.
I was taught that if 0.9999… didn’t equal 1 there would have to be a number that exists between the two. Since there isn’t, then 0.9999…=1
Not even a number between, but there is no distance between the two. There is no value X for 1-x = 0.9~
We can’t notate 0.0~ …01 in any way.
Divide 1 by 3: 1÷3=0.3333…
Multiply the result by 3 reverting the operation: 0.3333… x 3 = 0.9999… or just 1
0.9999… = 1
You’re just rounding up an irrational number. You have a non terminating, non repeating number, that will go on forever, because it can never actually get up to its whole value.
1/3 is a rational number, because it can be depicted by a ratio of two integers. You clearly don’t know what you’re talking about, you’re getting basic algebra level facts wrong. Maybe take a hint and read some real math instead of relying on your bad intuition.
1/3 is rational.
.3333… is not. You can’t treat fractions the same as our base 10 number system. They don’t all have direct conversions. Hence, why you can have a perfect fraction of a third, but not a perfect 1/3 written out in base 10.
0.333… exactly equals 1/3 in base 10. What you are saying is factually incorrect and literally nonsense. You learn this in high school level math classes. Link literally any source that supports your position.
.333… is rational.
at least we finally found your problem: you don’t know what rational and irrational mean. the clue is in the name.
TBH the name is a bit misleading. Same for “real” numbers. And oh so much more so for “normal numbers”.
not really. i get it because we use rational to mean logical, but that’s not what it means here. yeah, real and normal are stupid names but rational numbers are numbers that can be represented as a ratio of two numbers. i think it’s pretty good.
non repeating
it’s literally repeating
In this context, yes, because of the cancellation on the fractions when you recover.
1/3 x 3 = 1
I would say without the context, there is an infinitesimal difference. The approximation solution above essentially ignores the problem which is more of a functional flaw in base 10 than a real number theory issue
The context doesn’t make a difference
In base 10 --> 1/3 is 0.333…
In base 12 --> 1/3 is 0.4
But they’re both the same number.
Base 10 simply is not capable of displaying it in a concise format. We could say that this is a notation issue. No notation is perfect. Base 10 has some confusing implications
They’re different numbers. Base 10 isn’t perfect and can’t do everything just right, so you end up with irrational numbers that go on forever, sometimes.
This seems to be conflating
0.333...3with0.333...One is infinitesimally close to 1/3, the other is a decimal representation of 1/3. Indeed, if1-0.999...resulted in anything other than 0, that would necessarily be a number with more significant digits than0.999...which would mean that thefailed to be an infinite repetition.
Unfortunately not an ideal proof.
It makes certain assumptions:
- That a number 0.999… exists and is well-defined
- That multiplication and subtraction for this number work as expected
Similarly, I could prove that the number which consists of infinite 9’s to the left of the decimal separator is equal to -1:
...999.0 = x ...990.0 = 10x Calculate x - 10x: x - 10x = ...999.0 - ...990.0 -9x = 9 x = -1And while this is true for 10-adic numbers, it is certainly not true for the real numbers.
While I agree that my proof is blunt, yours doesn’t prove that .999… is equal to -1. With your assumption, the infinite 9’s behave like they’re finite, adding the 0 to the end, and you forgot to move the decimal point in the beginning of the number when you multiplied by 10.
x=0.999…999
10x=9.999…990 assuming infinite decimals behave like finite ones.
Now x - 10x = 0.999…999 - 9.999…990
-9x = -9.000…009
x = 1.000…001
Thus, adding or subtracting the infinitesimal makes no difference, meaning it behaves like 0.
Edit: Having written all this I realised that you probably meant the infinitely large number consisting of only 9’s, but with infinity you can’t really prove anything like this. You can’t have one infinite number being 10 times larger than another. It’s like assuming division by 0 is well defined.
0a=0b, thus
a=b, meaning of course your …999 can equal -1.
Edit again: what my proof shows is that even if you assume that .000…001≠0, doing regular algebra makes it behave like 0 anyway. Your proof shows that you can’t to regular maths with infinite numbers, which wasn’t in question. Infinity exists, the infinitesimal does not.
Yes, but similar flaws exist for your proof.
The algebraic proof that 0.999… = 1 must first prove why you can assign 0.999… to x.
My “proof” abuses algebraic notation like this - you cannot assign infinity to a variable. After that, regular algebraic rules become meaningless.
The proper proof would use the definition that the value of a limit approaching another value is exactly that value. For any epsilon > 0, 0.999… will be within the epsilon environment of 1 (= the interval 1 ± epsilon), therefore 0.999… is 1.
The explanation I’ve seen is that … is notation for something that can be otherwise represented as sums of infinite series.
In the case of 0.999…, it can be shown to converge toward 1 with the convergence rule for geometric series.
If |r| < 1, then:
ar + ar² + ar³ + … = ar / (1 - r)
Thus:
0.999… = 9(1/10) + 9(1/10)² + 9(1/10)³ + …
= 9(1/10) / (1 - 1/10)
= (9/10) / (9/10)
= 1
Just for fun, let’s try 0.424242…
0.424242… = 42(1/100) + 42(1/100)² + 42(1/100)³
= 42(1/100) / (1 - 1/100)
= (42/100) / (99/100)
= 42/99
= 0.424242…
So there you go, nothing gained from that other than seeing that 0.999… is distinct from other known patterns of repeating numbers after the decimal point.
The explanation I’ve seen is that … is notation for something that can be otherwise represented as sums of infinite series
The ellipsis notation generally refers to repetition of a pattern. Either ad infinitum, or up to some terminus. In this case we have a non-terminating decimal.
In the case of 0.999…, it can be shown to converge toward 1
0.999… is a real number, and not any object that can be said to converge. It is exactly 1.
So there you go, nothing gained from that other than seeing that 0.999… is distinct from other known patterns of repeating numbers after the decimal point
In what way is it distinct?
And what is a ‘repeating number’? Did you mean ‘repeating decimal’?The ellipsis notation generally refers to repetition of a pattern.
Ok. In mathematical notation/context, it is more specific, as I outlined.
This technicality is often brushed over or over simplified by math teachers and courses until or unless you take some more advanced courses.
Context matters, here’s an example:
Generally, pdf denotes the file format specific to adobe reader, while in the context of many modern online videos/discussions, it has become a colloquialism to be able to discuss (accused or confirmed) pedophiles and be able to avoid censorship or demonetization.
0.999… is a real number, and not any object that can be said to converge. It is exactly 1.
Ok. Never said 0.999… is not a real number. Yep, it is exactly 1 because solving the equation it truly represents, a geometric series, results in 1. This solution is obtained using what is called the convergence theorem or rule, as I outlined.
In what way is it distinct?
0.424242… solved via the convergence theorem simply results in itself, as represented in mathematical nomenclature.
0.999… does not again result in 0.999…, but results to 1, a notably different representation that causes the entire discussion in this thread.
And what is a ‘repeating number’? Did you mean ‘repeating decimal’?
I meant what I said: “know patterns of repeating numbers after the decimal point.”
Perhaps I should have also clarified known finite patterns to further emphasize the difference between rational and irrational numbers.
EDIT: You used a valid and even more mathematically esoteric method to demonstrate the same thing I demonstrated elsewhere in this thread, I have no idea why you are taking issue with what I’ve said.
Ok. In mathematical notation/context, it is more specific, as I outlined.
It is not. You will routinely find it used in cases where your explanation does not apply, such as to denote the contents of a matrix.
Furthermore, we can define real numbers without defining series. In such contexts, your explanation also doesn’t work until we do defines series of rational numbers.
Ok. Never said 0.999… is not a real number
In which case it cannot converge to anything on account of it not being a function or any other things that can be said to converge.
because solving the equation it truly represents, a geometric series, results in 1
A series is not an equation.
This solution is obtained using what is called the convergence theorem
What theorem? I have never heard of ‘the convergence theorem’.
0.424242… solved via the convergence theorem simply results in itself
What do you mean by ‘solving’ a real number?
0.999… does not again result in 0.999…, but results to 1
In what way does it not ‘result in 0.999…’ when 0.999… = 1?
You seem to not understand what decimals are, because while decimals (which are representations of real numbers) ‘0.999…’ and ‘1’ are different, they both refer to the same real number. We can use expressions ‘0.999…’ and ‘1’ interchangeably in the context of base 10. In other bases, we can easily also find similar pairs of digital representations that refer to the same numbers.
I meant what I said: “know patterns of repeating numbers after the decimal point.”
What we have after the decimal point are digits. OTOH, sure, we can treat them as numbers, but still, this is not a common terminology. Furthermore, ‘repeating number’ is not a term in any sort of commonly-used terminology in this context.
The actual term that you were looking for is ‘repeating decimal’.
Perhaps I should have also clarified known finite patterns to further emphasize the difference between rational and irrational numbers
No irrational number can be represented by a repeating decimal.
https://www2.kenyon.edu/Depts/Math/Paquin/GeomSeriesCalcB.pdf
Here’s a standard introduction to the concept of the Convergence/Divergence Theorem of Geometric Series, starts on page 2.
Its quite common for this to be referred to as the convergence test or rule or theorem by teachers and TA’s.
Now, ask yourself this question, ‘is 0.999…, or any real number for that matter, a series?’. The answer to that question is ‘no’.
You seem to be extremely confused, and think that the terms ‘series’ and ‘the sum of a series’ mean the same thing. They do not. 0.999… is the sum of the series 9/10+9/100+9/1000+…, and not a series itself.
EDIT: Also, the author does abuse the notations somewhat when she says ‘1+1/2+1/4 = 2’ is a geometric series, as the geometric series 1+1/2+1/4+… does not equal 2, because a series is either just a formal sum, a sequence of its terms, or, in German math traditions, a sequence of its partial sums. It is the sum of the series 1+1/2+1/4+… that is equal to 2. The confusion is made worse by the fact that sums of series and the series themselves are often denoted in the same way. However, again, those are different things.
Would you mind providing a snippet with the definition of the term ‘series’ that she provides?EDIT 2: Notably, that document has no theorem that is called ‘convergence theorem’ or ‘the convergence theorem’. The only theorem that is present there is the one on convergence and divergence of geometric series.
deleted by creator
X=.5555…
10x=5.5555…
Subtract x from both sides.
9x=5
X=1 .5555 must equal 1.
There it isn’t. Because that math is bullshit.
x = 5/9 is not 9/9. 5/9 = .55555…
You’re proving that 0.555… equals 5/9 (which it does), not that it equals 1 (which it doesn’t).
It’s absolutely not the same result as x = 0.999… as you claim.
?
Where did you get 9x=5 -> x=1
and 5/9 is 0.555… so it checks out.Quick maffs
Lol what? How did you conclude that if
9x = 5thenx = 1? Surely you didn’t pass algebra in high school, otherwise you could see that gettingxfrom9x = 5requires dividing both sides by 9, which yieldsx = 5/9, i.e.0.555... = 5/9sincex = 0.555....Also, you shouldn’t just use uppercase
Xin place of lowercasexor vice versa. Case is usually significant for variable names.
Okay, but it equals one.
No, it equals 0.999…
2/9 = 0.222… 7/9 = 0.777…
0.222… + 0.777… = 0.999… 2/9 + 7/9 = 1
0.999… = 1
No, it equals 1.
Similarly, 1/3 = 0.3333…
So 3 times 1/3 = 0.9999… but also 3/3 = 1Another nice one:
Let x = 0.9999… (multiply both sides by 10)
10x = 9.99999… (substitute 0.9999… = x)
10x = 9 + x (subtract x from both sides)
9x = 9 (divide both sides by 9)
x = 1My favorite thing about this argument is that not only are you right, but you can prove it with math.
you can prove it with math
Not a proof, just wrong. In the “(substitute 0.9999… = x)” step, it was only done to one side, not both (the left side would’ve become 9.99999), therefore wrong.
They multiplied both sides by 10.
0.9999… times 10 is 9.9999…
X times 10 is 10x.
X times 10 is 10x
10x is 9.9999999…
As I said, they didn’t substitute on both sides, only one, thus breaking the rules around rearranging algebra. Anything you do to one side you have to do to the other.
The substitution property of equality is a part of its definition; you can substitute anywhere.
you can substitute anywhere
And if you are rearranging algebra you have to do the exact same thing on both sides, always
Except it doesn’t. The math is wrong. Do the exact same formula, but use .5555… instead of .9999…
Guess it turns out .5555… is also 1.
Lol you can’t do math apparently, take a logic course sometime
Let x=0.555…
10x=5.555…
10x=5+x
9x=5
x=5/9=0.555…
Oh honey
you have to do this now
That’s the best explanation of this I’ve ever seen, thank you!
That’s more convoluted than the 1/3, 2/3, 3/3 thing.
3/3 = 0.99999…
3/3 = 1
If somebody still wants to argue after that, don’t bother.
Nah that explanation is basically using an assumption to prove itself. You need to first prove that 1/3 does in fact equal .3333… which can be done using the ‘convoluted’ but not so convoluted proof
If you can’t do it without fractions or a … then it can’t be done.
We’ve found a time traveller from ancient Greece…
Edit: sorry. I mean we’ve found a time traveller from ancient Mesopotamia.
1/3=0.333…
2/3=0.666…
3/3=0.999…=1
Fractions and base 10 are two different systems. You’re only approximating what 1/3 is when you write out 0.3333…
The … is because you can’t actually make it correct in base 10.
The fractions are still in base 10 lmfao literally what the fuck are you talking about and where are getting this from?
You keep getting basic shit wrong, and it makes you look dumb. Stop talking and go read a wiki.
What exactly do you think notations like 0.999… and 0.333… mean?
That it repeats forever, to no end. Because it can never actually be correct, just that the difference becomes insignificant.
Sure, let’s do it in base 3. 3 in base 3 is 10, and 3^(-1) is 10^(-1), so:
1/3 in base 10 = 1/10 in base 3
0.3… in base 10 = 0.1 in base 3Multiply by 3 on both sides:
3 × 0.3… in base 10 = 10 × 0.1 in base 3
0.9… in base 10 = 1 in base 3.But 1 in base 3 is also 1 in base 10, so:
0.9… in base 10 = 1 in base 10
You’re having to use … to make your conversion again. If you need to to an irrational number to make your equation correct, it isn’t really correct.
Sure, when you start decoupling the numbers from their actual values. The only thing this proves is that the fraction-to-decimal conversion is inaccurate. Your floating points (and for that matter, our mathematical model) don’t have enough precision to appropriately model what the value of 7/9 actually is. The variation is negligible though, and that’s the core of this, is the variation off what it actually is is so small as to be insignificant and, really undefinable to us - but that doesn’t actually matter in practice, so we just ignore it or convert it. But at the end of the day 0.999… does not equal 1. A number which is not 1 is not equal to 1. That would be absurd. We’re just bad at converting fractions in our current mathematical understanding.
Edit: wow, this has proven HIGHLY unpopular, probably because it’s apparently incorrect. See below for about a dozen people educating me on math I’ve never heard of. The “intuitive” explanation on the Wikipedia page for this makes zero sense to me largely because I don’t understand how and why a repeating decimal can be considered a real number. But I’ll leave that to the math nerds and shut my mouth on the subject.
You are just wrong.
The rigorous explanation for why 0.999…=1 is that 0.999… represents a geometric series of the form 9/10+9/10^2+… by definition, i.e. this is what that notation literally means. The sum of this series follows by taking the limit of the corresponding partial sums of this series (see here) which happens to evaluate to 1 in the particular case of 0.999… this step is by definition of a convergent infinite series.
The only thing this proves is that the fraction-to-decimal conversion is inaccurate.
No number is getting converted, it’s the same number in both cases but written in a different representation. 4 is also the same number as IV, no conversion going on it’s still the natural number elsewhere written
S(S(S(S(Z)))). Also decimal representation isn’t inaccurate, it just happens to have multiple valid representations for the same number.A number which is not 1 is not equal to 1.
Good then that 0.999… and 1 are not numbers, but representations.
Lol I fucking love that successor of zero
It still equals 1, you can prove it without using fractions:
x = 0.999…
10x = 9.999…
10x = 9 + 0.999…
10x = 9 + x
9x = 9
x = 1
There’s even a Wikipedia page on the subject
I hate this because you have to subtract .99999… from 10. Which is just the same as saying 10 - .99999… = 9
Which is the whole controversy but you made it complicated.
It would be better just to have them do the long subtraction
If they don’t get it and keep trying to show you how you are wrong they will at least be out of your hair until forever.
You don’t subtract from 10, but from 10x0.999… I mean your statement is also true but it just proves the point further.
No, you do subtract from 9.999999…
deleted by creator
Do that same math, but use .5555… instead of .9999…
Have you tried it? You get 0.555… which kinda proves the point does it not?
???
Not sure what you’re aiming for. It proves that the setup works, I suppose.
x = 0.555…
10x = 5.555…
10x = 5 + 0.555…
10x = 5+x
9x = 5
x = 5/9
5/9 = 0.555…
So it shows that this approach will indeed provide a result for x that matches what x is supposed to be.
Hopefully it helped?
If they aren’t equal, there should be a number in between that separates them. Between 0.1 and 0.2 i can come up with 0.15. Between 0.1 and 0.15 is 0.125. You can keep going, but if the numbers are equal, there is nothing in between. There’s no gap between 0.1 and 0.1, so they are equal.
What number comes between 0.999… and 1?
(I used to think it was imprecise representations too, but this is how it made sense to me :)
My brother. You are scared of infinities. Look up the infinite hotel problem. I will lay it out for you if you are interested.
Image you are incharge of a hotel and it has infinite rooms. Currently your hotel is at full capacity… Meaning all rooms are occupied. A new guest arrives. What do you do? Surely your hotel is full and you can’t take him in… Right? WRONG!!! You tell the resident of room 1 to move to room 2, you tell the resident of room 2 to move to room 3 and so on… You tell the resident of room n to move to room n+1. Now you have room 1 empty
But sir… How did I create an extra room? You didn’t. The question is the same as asking yourself that is there a number for which n+1 doesn’t exist. The answer is no… I can always add 1.
Infinity doesn’t behave like other numbers since it isn’t technically a number.
So when you write 0.99999… You are playing with things that aren’t normal. Maths has come with fuckall ways to deal with stuff like this.
Well you may say, this is absurd… There is nothing in reality that behaves this way. Well yes and no. You know how the building blocks of our universe obey quantum mechanics? The equations contain lots of infinities but only at intermediate steps. You have to “renormalise” them to make them go away. Nature apparently has infinities but likes to hide the from us.
The infinity problem is so fucked up. You know the reason physics people are unable to quantize gravity? Surely they can do the same thing to gravity as they did to say electromagnetic force? NOPE. Gravitation doesn’t normalise. You get left with infinities in your final answer.
Anyways. Keep on learning, the world has a lot of information and it’s amazing. And the only thing that makes us human is the ability to learn and grow from it. I wish you all the very best.
But sir… How did I create an extra room? You didn’t.
When Hilbert runs the hotel, sure, ok. Once he sells the whole thing to an ultrafinitist however you suddenly notice that there’s a factory there and all the rooms are on rails and infinity means “we have a method to construct arbitrarily more rooms”, but they don’t exist before a guest arrives to occupy them.
It’s a correct proof.
One way to think about this is that we represent numbers in different ways. For example, 1 can be 1.0, or a single hash mark, or a dot, or 1/1, or 10/10. All of them point to some platonic ideal world version of the concept of the number 1.
What we have here is two different representations of the same number that are in a similar representation. 1 and 0.999… both point to the same concept.
I strongly agree with you, and while the people replying aren’t wrong, they’re arguing for something that I don’t think you said.
1/3 ≈ 0.333… in the same way that approximating a circle with polygons of increasing side number has a limit of a circle, but will never yeild a circle with just geometry.
0.999… ≈ 1 in the same way that shuffling infinite people around an infinite hotel leaves infinite free rooms, but if you try to do the paperwork, no one will ever get anywhere.
Decimals require you to check the end of the number to see if you can round up, but there never will be an end. Thus we need higher mathematics to avoid the halting problem. People get taught how decimals work, find this bug, and then instead of being told how decimals are broken, get told how they’re wrong for using the tools they’ve been taught.
If we just accept that decimals fail with infinite steps, the transition to new tools would be so much easier, and reflect the same transition into new tools in other sciences. Like Bohr’s Atom, Newton’s Gravity, Linnaean Taxonomy, or Comte’s Positivism.
Decimals require you to check the end of the number to see if you can round up, but there never will be an end.
The character sequence “0.999…” is finite and you know you can round up because you’ve got those three dots at the end. I agree that decimals are a shit representation to formalise rational numbers in but it’s not like using them causes infinite loops. Unless you insist on writing them, that is. You can compute with infinities just fine as long as you keep them symbolic.
That only breaks down with the reals where equality is fundamentally incomputable. Equality of the rationals and approximate equality of reals is perfectly computable though, the latter meaning that you can get equality to arbitrary, but not actually infinite, precision. You can specify a number of digits you want, you can say “don’t take longer than ten seconds to compute”, any kind of bound. Once the precision goes down to plank lengths I think any reasonable engineer would build a bridge with it.
…sometimes I do think that all those formalists with all those fancy rules about fancy limits are actually way more confused about infinity than freshman CS students.
Eh, if you need special rules for 0.999… because the special rules for all other repeating decimals failed, I think we should just accept that the system doesn’t work here. We can keep using the workaround, but stop telling people they’re wrong for using the system correctly.
The deeper understanding of numbers where 0.999… = 1 is obvious needs a foundation of much more advanced math than just decimals, at which point decimals stop being a system and are just a quirky representation.
Saying decimals are a perfect system is the issue I have here, and I don’t think this will go away any time soon. Mathematicians like to speak in absolutely terms where everything is either perfect or discarded, yet decimals seem to be too simple and basal to get that treatment. No one seems to be willing to admit the limitations of the system.
Noone in the right state of mind uses decimals as a formalisation of numbers, or as a representation when doing arithmetic.
But the way I learned decimal division and multiplication in primary school actually supported periods. Spotting whether the thing will repeat forever can be done in finite time. Constant time, actually.
The deeper understanding of numbers where 0.999… = 1 is obvious needs a foundation of much more advanced math than just decimals
No. If you can accept that 1/3 is 0.333… then you can multiply both sides by three and accept that 1 is 0.99999… Primary school kids understand that. It’s a bit odd but a necessary consequence if you restrict your notation from supporting an arbitrary division to only divisions by ten. And that doesn’t make decimal notation worse than rational notation, or better, it makes it different, rational notation has its own issues like also not having unique forms (2/6 = 1/3) and comparisons (larger/smaller) not being obvious. Various arithmetic on them is also more complicated.
The real take-away is that depending on what you do, one is more convenient than the other. And that’s literally all that notation is judged by in maths: Is it convenient, or not.
The system works perfectly, it just looks wonky in base 10. In base 3 0.333… looks like 0.1, exactly 0.1
That does very accurately sum up my understanding of the matter, thanks. I haven’t been adding on to any of the other conversation in order to avoid putting my foot in my mouth further, but you’ve pretty much hit the nail on the head here. And the higher mathematics required to solve this halting problem are beyond me.
THAT’S EXACTLY WHAT I SAID.
deleted by creator
I thought the muscular guys were supposed to be right in these memes.
He is right. 1 approximates 1 to any accuracy you like.
Is it true to say that two numbers that are equal are also approximately equal?
I recall an anecdote about a mathematician being asked to clarify precisely what he meant by “a close approximation to three”. After thinking for a moment, he replied “any real number other than three”.
“Approximately equal” is just a superset of “equal” that also includes values “acceptably close” (using whatever definition you set for acceptable).
Unless you say something like:
a ≈ b ∧ a ≠ b
which implies a is close to b but not exactly equal to b, it’s safe to presume that a ≈ b includes the possibility that a = b.
Can I get a citation on this? Because it doesn’t pass the sniff test for me. https://en.wikipedia.org/wiki/Approximation
Sure! See ISO-80000-2
Here’s a link: https://cdn.standards.iteh.ai/samples/64973/329519100abd447ea0d49747258d1094/ISO-80000-2-2019.pdf
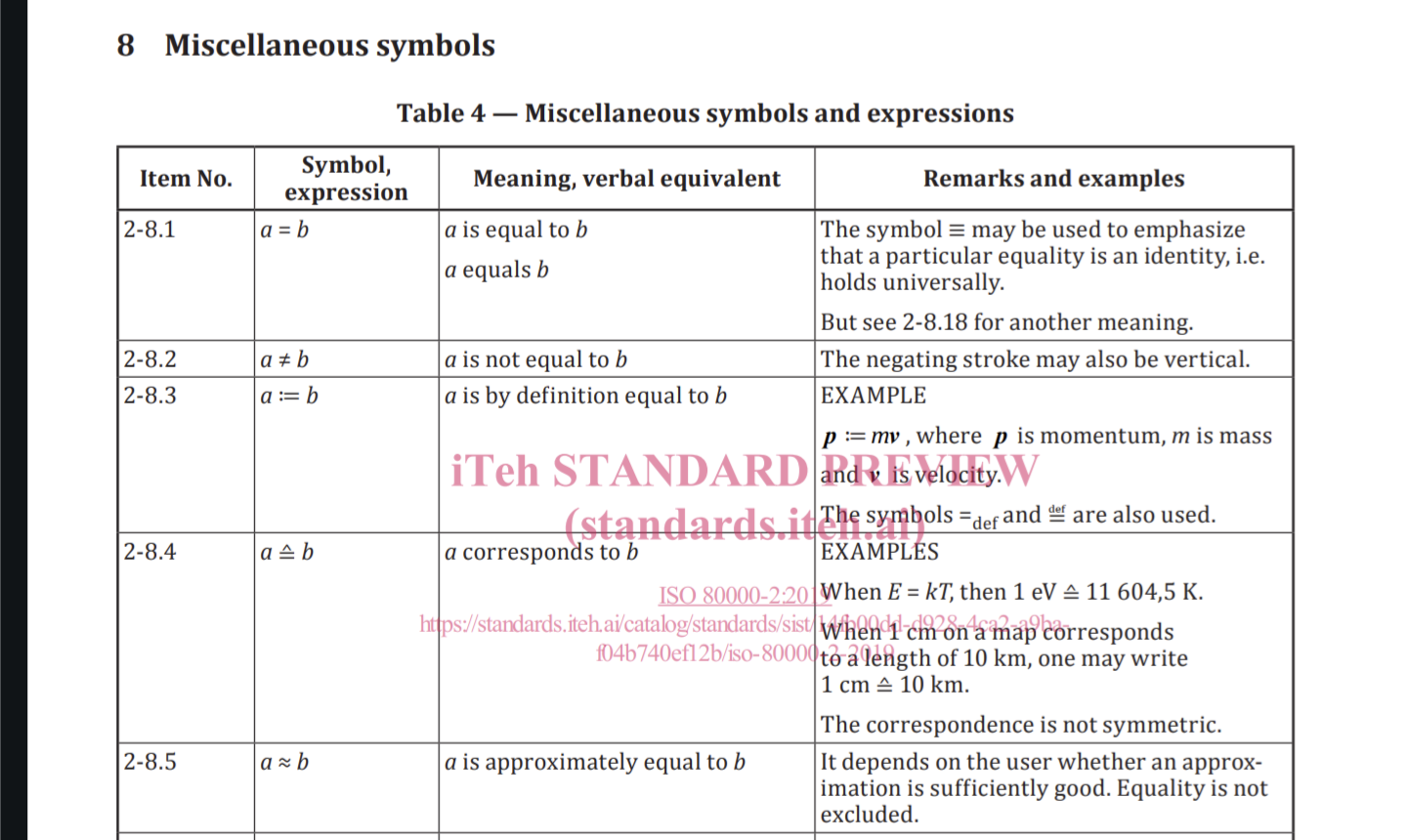
ISO is not a source for mathematical definitions
It’s a definition from a well-respected global standards organization. Can you name a source that would provide a more authoritative definition than the ISO?
There’s no universally correct definition for what the ≈ symbol means, and if you write a paper or a proof or whatever, you’re welcome to define it to mean whatever you want in that context, but citing a professional standards organization seems like a pretty reliable way to find a commonly-accepted and understood definition.
assert np.isClose(3, 3)
Yes, informally in the sense that the error between the two numbers is “arbitrarily small”. Sometimes in introductory real analysis courses you see an exercise like: “prove if x, y are real numbers such that x=y, then for any real epsilon > 0 we have |x - y| < epsilon.” Which is a more rigorous way to say roughly the same thing. Going back to informality, if you give any required degree of accuracy (epsilon), then the error between x and y (which are the same number), is less than your required degree of accuracy
It depends on the convention that you use, but in my experience yes; for any equivalence relation, and any metric of “approximate” within the context of that relation, A=B implies A≈B.
Nah. They are supposed to not care about stuff and just roll with it without any regrets.
It’s just like the wojak crying with the mask on, but not crying behind it.
There’s plenty of cases of memes where the giga chad is just plainly wrong, but they just don’t care. But it’s not supposed to be in a troll way. The giga chad applies what it believes in. If you want a troll, there’s troll face, who speak with the confidence of a giga chad, but know he is bullshiting
0.9<overbar.> is literally equal to 1
There’s a Real Analysis proof for it and everything.
Basically boils down to
- If 0.(9) != 1 then there must be some value between 0.(9) and 1.
- We know such a number cannot exist, because for any given discrete value (say 0.999…9) there is a number (0.999…99) that is between that discrete value and 0.(9)
- Therefore, no value exists between 0.(9) and 1.
- So 0.(9) = 1
Even simpler: 1 = 3 * 1/3
1/3 =0.333333…
1/3 + 1/3 + 1/3 = 0.99999999… = 1
Even simpler
0.99999999… = 1
But you’re just restating the premise here. You haven’t proven the two are equal.
1/3 =0.333333…
This step
1/3 + 1/3 + 1/3 = 0.99999999…
And this step
Aren’t well-defined. You’re relying on division short-hand rather than a real proof.
ELI5
Mostly boils down to the pedantry of explaining why 1/3 = 0.(3) and what 0.(3) actually means.
the explanation (not proof tbf) that actually satisfies my brain is that we’re dealing with infinite repeating digits here, which is what allows something that on the surface doesn’t make sense to actually be true.
Infinite repeating digits produce what is understood as a Limit. And Limits are fundamental to proof-based mathematics, when your goal is to demonstrate an infinite sum or series has a finite total.
That actually makes sense, thank you.
0.9 is most definitely not equal to 1
Hence the overbar. Lemmy should support LaTeX for real though
Oh, that’s not even showing as a missing character, to me it just looks like 0.9
At least we agree 0.99… = 1
Oh lol its rendering as HTML for you.
If 0.999… < 1, then that must mean there’s an infinite amount of real numbers between 0.999… and 1. Can you name a single one of these?
Sure 0.999…95
Just kidding, the guy on the left is correct.
You got me
(0.999… + 1) / 2
That number happens to be exactly 1
Remember when US politicians argued about declaring Pi to 3?
Would have been funny seeing the world go boink in about a week.
To everyone who might not have heard about that before: It was an attempt to introduce it as a bill in Indiana:
https://en.m.wikipedia.org/w/index.php?title=Indiana_pi_bill
the bill’s language and topic caused confusion; a member proposed that it be referred to the Finance Committee, but the Speaker accepted another member’s recommendation to refer the bill to the Committee on Swamplands, where the bill could “find a deserved grave”.
An assemblyman handed him the bill, offering to introduce him to the genius who wrote it. He declined, saying that he already met as many crazy people as he cared to.
I hope medicine in 1897 was up to the treatment of these burns.
Do you think Goodwin could treat the burns himself?
I’m sure he would have believed he could.
I prefer my pi to be in duodecimal anyway. 3.184809493B should get you to where you need to go.
Some software can be pretty resilient. I ended up watching this video here recently about running doom using different values for the constant pi that was pretty nifty.
deleted by creator
You didn’t even read the first paragraph of that article LMAO
This is why we can’t have nice things like dependable protection from fall damage while riding a boat in Minecraft.
Reals are just point cores of dressed Cauchy sequences of naturals (think of it as a continually constructed set of narrowing intervals “homing in” on the real being constructed). The intervals shrink at the same rate generally.
1!=0.999 iff we can find an n, such that the intervals no longer overlap at that n. This would imply a layer of absolute infinite thinness has to exist, and so we have reached a contradiction as it would have to have a width smaller than every positive real (there is no smallest real >0).
Therefore 0.999…=1.
However, we can argue that 1 is not identity to 0.999… quite easily as they are not the same thing.
This does argue that this only works in an extensional setting (which is the norm for most mathematics).
Easiest way to prove it:
1 = 3/3 = 1/3 * 3 = 0.333… * 3 = 0.999…
Ehh, completed infinities give me wind…
deleted by creator
Thanks for the bedtime reading!
I mostly deal with foundations of analysis, so this could be handy.
Are we still doing this 0.999… thing? Why, is it that attractive?
People generally find it odd and unintuitive that it’s possible to use decimal notation to represent 1 as .9~ and so this particular thing will never go away. When I was in HS I wowed some of my teachers by doing proofs on the subject, and every so often I see it online. This will continue to be an interesting fact for as long as decimal is used as a canonical notation.
Welp, I see. Still, this is way too much recurting of a pattern.
The rules of decimal notation don’t sipport infinite decimals properly. In order for a 9 to roll over into a 10, the next smallest decimal needs to roll over first, therefore an infinite string of anything will never resolve the needed discrete increment.
Thus, all arguments that 0.999… = 1 must use algebra, limits, or some other logic beyond decimal notation. I consider this a bug with decimals, and 0.999… = 1 to be a workaround.
don’t sipport infinite decimals properly
Please explain this in a way that makes sense to me (I’m an algebraist). I don’t know what it would mean for infinite decimals to be supported “properly” or “improperly”. Furthermore, I’m not aware of any arguments worth taking seriously that don’t use logic, so I’m wondering why that’s a criticism of the notation.
Decimal notation is a number system where fractions are accomodated with more numbers represeting smaller more precise parts. It is an extension of the place value system where very large tallies can be expressed in a much simpler form.
One of the core rules of this system is how to handle values larger than the highest digit, and lower than the smallest. If any place goes above 9, set that place to 0 and increment the next place by 1. If any places goes below 0, increment the place by (10) and decrement the next place by one (this operation uses a non-existent digit, which is also a common sticking point).
This is the decimal system as it is taught originally. One of the consequences of it’s rules is that each digit-wise operation must be performed in order, with a beginning and an end. Thus even getting a repeating decimal is going beyond the system. This is usually taught as special handling, and sometimes as baby’s first limit (each step down results in the same digit, thus it’s that digit all the way down).
The issue happens when digit-wise calculation is applied to infinite decimals. For most operations, it’s fine, but incrementing up can only begin if a digit goes beyong 9, which never happens in the case of 0.999… . Understanding how to resolve this requires ditching the digit-wise method and relearing decimals and a series of terms, and then learning about infinite series. It’s a much more robust and applicable method, but a very different method to what decimals are taught as.
Thus I say that the original bitwise method of decimals has a bug in the case of incrementing infinite sequences. There’s really only one number where this is an issue, but telling people they’re wrong for using the tools as they’ve been taught isn’t helpful. Much better to say that the tool they’re using is limited in this way, then showing the more advanced method.
That’s how we teach Newtonian Gravity and then expand to Relativity. You aren’t wrong for applying newtonian gravity to mercury, but the tool you’re using is limited. All models are wrong, but some are useful.
Said a simpler way:
1/3= 0.333…
1/3 + 1/3 = 0.666… = 0.333… + 0.333…
1/3 + 1/3 + 1/3 = 1 = 0.333… + 0.333… + 0.333…
The quirk you mention about infinite decimals not incrementing properly can be seen by adding whole number fractions together.
I can’t help but notice you didn’t answer the question.
each digit-wise operation must be performed in order
I’m sure I don’t know what you mean by digit-wise operation, because my conceptuazation of it renders this statement obviously false. For example, we could apply digit-wise modular addition base 10 to any pair of real numbers and the order we choose to perform this operation in won’t matter. I’m pretty sure you’re also not including standard multiplication and addition in your definition of “digit-wise” because we can construct algorithms that address many different orders of digits, meaning this statement would also then be false. In fact, as I lay here having just woken up, I’m having a difficult time figuring out an operation where the order that you address the digits in actually matters.
Later, you bring up “incrementing” which has no natural definition in a densely populated set. It seems to me that you came up with a function that relies on the notation we’re using (the decimal-increment function, let’s call it) rather than the emergent properties of the objects we’re working with, noticed that the function doesn’t cover the desired domain, and have decided that means the notation is somehow improper. Or maybe you’re saying that the reason it’s improper is because the advanced techniques for interacting with the system are dissimilar from the understanding imparted by the simple techniques.
In base 10, if we add 1 and 1, we get the next digit, 2.
In base 2, if we add 1 and 1 there is no 2, thus we increment the next place by 1 getting 10.
We can expand this to numbers with more digits: 111(7) + 1 = 112 = 120 = 200 = 1000
In base 10, with A representing 10 in a single digit: 199 + 1 = 19A = 1A0 = 200
We could do this with larger carryover too: 999 + 111 = AAA = AB0 = B10 = 1110 Different orders are possible here: AAA = 10AA = 10B0 = 1110
The “carry the 1” process only starts when a digit exceeds the existing digits. Thus 192 is not 2Z2, nor is 100 = A0. The whole point of carryover is to keep each digit within the 0-9 range. Furthermore, by only processing individual digits, we can’t start carryover in the middle of a chain. 999 doesn’t carry over to 100-1, and while 0.999 does equal 1 - 0.001, (1-0.001) isn’t a decimal digit. Thus we can’t know if any string of 9s will carry over until we find a digit that is already trying to be greater than 9.
This logic is how basic binary adders work, and some variation of this bitwise logic runs in evey mechanical computer ever made. It works great with integers. It’s when we try to have infinite digits that this method falls apart, and then only in the case of infinite 9s. This is because a carry must start at the smallest digit, and a number with infinite decimals has no smallest digit.
Without changing this logic radically, you can’t fix this flaw. Computers use workarounds to speed up arithmetic functions, like carry-lookahead and carry-save, but they still require the smallest digit to be computed before the result of the operation can be known.
If I remember, I’ll give a formal proof when I have time so long as no one else has done so before me. Simply put, we’re not dealing with floats and there’s algorithms to add infinite decimals together from the ones place down using back-propagation. Disproving my statement is as simple as providing a pair of real numbers where doing this is impossible.
Are those algorithms taught to people in school?
Once again, I have no issue with the math. I just think the commonly taught system of decimal arithmetic is flawed at representing that math. This flaw is why people get hung up on 0.999… = 1.
Furthermore, I’m not aware of any arguments worth taking seriously that don’t use logic, so I’m wondering why that’s a criticism of the notation.
If you hear someone shout at a mob “mathematics is witchcraft, therefore, get the pitchforks” I very much recommend taking that argument seriously no matter the logical veracity.
Fair, but that still uses logic, it’s just using false premises. Also, more than the argument what I’d be taking seriously is the threat of imminent violence.
But is it a false premise? It certainly passes Occam’s razor: “They’re witches, they did it” is an eminently simple explanation.
By definition, mathematics isn’t witchcraft (most witches I know are pretty bad at math). Also, I think you need to look more deeply into Occam’s razor.
By definition, all sufficiently advanced mathematics is isomorphic to witchcraft. (*vaguely gestures at numerology as proof*). Also Occam’s razor has never been robust against reductionism: If you are free to reduce “equal explanatory power” to arbitrary small tunnel vision every explanation becomes permissible, and taking, of those, the simplest one probably doesn’t match with the holistic view. Or, differently put: I think you need to look more broadly onto Occam’s razor :)
i don’t think any number system can be safe from infinite digits. there’s bound to be some number for each one that has to be represented with them. it’s not intuitive, but that’s because infinity isn’t intuitive. that doesn’t mean there’s a problem there though. also the arguments are so simple i don’t understand why anyone would insist that there has to be a difference.
for me the simplest is:
1/3 = 0.333…
so
3×0.333… = 3×1/3
0.999… = 3/3
the problem is it makes my brain hurt
honestly that seems to be the only argument from the people who say it’s not equal. at least you’re honest about it.
by the way I’m not a mathematically adept person. I’m interested in math but i only understand the simpler things. which is fine. but i don’t go around arguing with people about advanced mathematics because I personally don’t get it.
the only reason I’m very confident about this issue is that you can see it’s equal with middle- or high-school level math, and that’s somehow still too much for people who are too confident about there being a magical, infinitely small number between 0.999… and 1.
to be clear I’m not arguing against you or disagreeing the fraction thing demonstrates what you’re saying. It just really bothers me when I think about it like my brain will not accept it even though it’s right in front of me it’s almost like a physical sensation. I think that’s what cognitive dissonance is. Fortunately in the real world this has literally never come up so I don’t have to engage with it.
no, i know and understand what you mean. as i said in my original comment; it’s not intuitive. but if everything in life were intuitive there wouldn’t be mind blowing discoveries and revelations… and what kind of sad life is that?
Any my argument is that 3 ≠ 0.333…
EDIT: 1/3 ≠ 0.333…
We’re taught about the decimal system by manipulating whole number representations of fractions, but when that method fails, we get told that we are wrong.
In chemistry, we’re taught about atoms by manipulating little rings of electrons, and when that system fails to explain bond angles and excitation, we’re told the model is wrong, but still useful.
This is my issue with the debate. Someone uses decimals as they were taught and everyone piles on saying they’re wrong instead of explaining the limitations of systems and why we still use them.
For the record, my favorite demonstration is useing different bases.
In base 10: 1/3 ≈ 0.333… 0.333… × 3 = 0.999…
In base 12: 1/3 = 0.4 0.4 × 3 = 1
The issue only appears if you resort to infinite decimals. If you instead change your base, everything works fine. Of course the only base where every whole fraction fits nicely is unary, and there’s some very good reasons we don’t use tally marks much anymore, and it has nothing to do with math.
you’re thinking about this backwards: the decimal notation isn’t something that’s natural, it’s just a way to represent numbers that we invented. 0.333… = 1/3 because that’s the way we decided to represent 1/3 in decimals. the problem here isn’t that 1 cannot be divided by 3 at all, it’s that 10 cannot be divided by 3 and give a whole number. and because we use the decimal system, we have to notate it using infinite repeating numbers but that doesn’t change the value of 1/3 or 10/3.
different bases don’t change the values either. 12 can be divided by 3 and give a whole number, so we don’t need infinite digits. but both 0.333… in decimal and 0.4 in base12 are still 1/3.
there’s no need to change the base. we know a third of one is a third and three thirds is one. how you notate it doesn’t change this at all.
I’m not saying that math works differently is different bases, I’m using different bases exactly because the values don’t change. Using different bases restates the equation without using repeating decimals, thus sidestepping the flaw altogether.
My whole point here is that the decimal system is flawed. It’s still useful, but trying to claim it is perfect leads to a conflict with reality. All models are wrong, but some are useful.
you said 1/3 ≠ 0.333… which is false. it is exactly equal. there’s no flaw; it’s a restriction in notation that is not unique to the decimal system. there’s no “conflict with reality”, whatever that means. this just sounds like not being able to wrap your head around the concept. but that doesn’t make it a flaw.
Let me restate: I am of the opinion that repeating decimals are imperfect representations of the values we use them to represent. This imperfection only matters in the case of 0.999… , but I still consider it a flaw.
I am also of the opinion that focusing on this flaw rather than the incorrectness of the person using it is a better method of teaching.
I accept that 1/3 is exactly equal to the value typically represented by 0.333… , however I do not agree that 0.333… is a perfect representation of that value. That is what I mean by 1/3 ≠ 0.333… , that repeating decimal is not exactly equal to that value.
Any my argument is that 3 ≠ 0.333…
After reading this, I have decided that I am no longer going to provide a formal proof for my other point, because odds are that you wouldn’t understand it and I’m now reasonably confident that anyone who would already understands the fact the proof would’ve supported.
Ah, typo. 1/3 ≠ 0.333…
It is my opinion that repeating decimals cannot properly represent the values we use them for, and I would rather avoid them entirely (kinda like the meme).
Besides, I have never disagreed with the math, just that we go about correcting people poorly. I have used some basic mathematical arguments to try and intimate how basic arithmetic is a limited system, but this has always been about solving the systemic problem of people getting caught by 0.999… = 1. Math proofs won’t add to this conversation, and I think are part of the issue.
Is it possible to have a coversation about math without either fully agreeing or calling the other stupid? Must every argument about even the topic be backed up with proof (a sociological one in this case)? Or did you just want to feel superior?
It is my opinion that repeating decimals cannot
Your opinion is incorrect as a question of definition.
I have never disagreed with the math
You had in the previous paragraph.
Is it possible to have a coversation about math without either fully agreeing or calling the other stupid?
Yes, however the problem is that you are speaking on matters that you are clearly ignorant. This isn’t a question of different axioms where we can show clearly how two models are incompatible but resolve that both are correct in their own contexts; this is a case where you are entirely, irredeemably wrong, and are simply refusing to correct yourself. I am an algebraist understanding how two systems differ and compare is my specialty. We know that infinite decimals are capable of representing real numbers because we do so all the time. There. You’re wrong and I’ve shown it via proof by demonstration. QED.
They are just symbols we use to represent abstract concepts; the same way I can inscribe a “1” to represent 3-2={ {} } I can inscribe “.9~” to do the same. The fact that our convention is occasionally confusing is irrelevant to the question; we could have a system whereby each number gets its own unique glyph when it’s used and it’d still be a valid way to communicate the ideas. The level of weirdness you can do and still have a valid notational convention goes so far beyond the meager oddities you’ve been hung up on here. Don’t believe me? Look up lambda calculus.
Meh, close enough.
I wish computers could calculate infinity
Computers can calculate infinite series as well as anyone else
As long as you have it forget the previous digit, you can bring up a new digit infinitely
0.(9)=0.(3)*3=1/3*3=1
Beautiful. Is that true or am I tricked?
0.3 is definitely NOT equal 1/3.
I guess 0.(3) means infinite 0.33333…. which is equal to 1/3
Yes, 0.(3) means repeating 3 in fractional part.
And there is entire wiki page on 0.(9)
Mathematics is built on axioms that have nothing to do with numbers yet. That means that things like decimal numbers need definitions. And in the definition of decimals is literally included that if you have only nines at a certain point behind the dot, it is the same as increasing the decimal in front of the first nine by one.
That’s not an axiom or definition, it’s a consequence of the axioms that define arithmetic and can therefore be proven.
There are versions of math where that isn’t true, with infinitesimals that are not equal to zero. So I think it is an axium rather than a provable conclusion.
Those versions have different axioms from which different things can be proven, but we don’t define 9.9 repeating as 1
That’s not what “axiom” means
That’s not how it’s defined. 0.99… is the limit of a sequence and it is precisely 1. 0.99… is the summation of infinite number of numbers and we don’t know how to do that if it isn’t defined. (0.9 + 0.09 + 0.009…) It is defined by the limit of the partial sums, 0.9, 0.99, 0.999… The limit of this sequence is 1. Sorry if this came out rude. It is more of a general comment.
I study mathematics at university and I remember it being in the definition, but since it follows from the sum’s limit anyways it probably was just there for claritie’s sake. So I guess we’re both right…
The decimals ‘0.999…’ and ‘1’ refer to the real numbers that are equivalence classes of Cauchy sequences of rational numbers (0.9, 0.99, 0.999,…) and (1, 1, 1,…) with respect to the relation R: (aRb) <=> (lim(a_n-b_n) as n->inf, where a_n and b_n are the nth elements of sequences a and b, respectively).
For a = (1, 1, 1,…) and b = (0.9, 0.99, 0.999,…) we have lim(a_n-b_n) as n->inf = lim(1-sum(9/10^k) for k from 1 to n) as n->inf = lim(1/10^n) as n->inf = 0. That means that (1, 1, 1,…)R(0.9, 0.99, 0.999,…), i.e. that these sequences belong to the same equivalence class of Cauchy sequences of rational numbers with respect to R. In other words, the decimals ‘0.999…’ and ‘1’ refer to the same real number. QED.